不偏標本分散の一致性を示してみる

本記事では省略されがちであったり, 正規分布であることを仮定してあったりすることの多い, 不偏標本分散の母分散の推定量としての一致性を証明していきます.

ことばの整理

本記事では $X$ の確率密度を $f(x)$ とし, $4$ 次モーメントを有界とします. すなわち $4$ 次までのモーメント
\begin{equation}
\mu_k = \int_\mathbb{R} x^kf(x)\,dx, \quad k =1,2,3,4
\end{equation}
が有限値であるものとします. このとき母平均 $\mu$ と母分散 $\sigma^2$ は,
$\begin{equation} \mu = \mu_1,\quad \sigma^2 = \mu_2 -\mu_1^2 \end{equation}$
と表すことができます. 自然数 $n > 1$ に対して, 同じ分布を持ちそれぞれ同士が異なる確率密度の列を $X_i,\, i=1,\cdots ,n$ としましょう. このとき母分散の不偏推定量として, 不偏標本分散を
\begin{equation}
s^2 =\dfrac{1}{n-1}\displaystyle\sum_{i=1}^n (X_i- \bar{X})^2
\end{equation}
と定義し, これが不偏推定量となっていることを前回記事 Rにたくさんさいころを振らせて、さいころの分散を求めてみる - わかばめにっきで示しました. 今回はこれが一致推定量となっていることも示していきます. つまり,

任意の $\varepsilon >0$ に対して, $n\rightarrow \infty$ のとき $P\left(|{s^2}-\sigma^2 |< \varepsilon \right) \rightarrow 1$ が成立すること

を証明します. 証明の鍵となるのは過去記事 Rにさいころをたくさん振らせて、さいころの平均を求めてみる - わかばめにっきで標本平均の一致性を示したときに使ったチェビシェフの不等式です. 一般的な形で改めて述べると,

確率変数 $Z$ に対して, 母平均と母分散をそれぞれ $E[Z], V[Z]$ とかく. このとき任意の $\varepsilon >0$ に対して,
\begin{equation}
P(|Z- E[Z]| \ge \varepsilon) \le V[Z]/\varepsilon^2
\end{equation}
が成立する

と言えます. $s^2$ に対してチェビシェフの不等式を用いることと, 前回証明した不偏性 $E[s^2]=\sigma^2$ により, $P(|s^2- \sigma^2| \ge \varepsilon) \le V[s^2]/\varepsilon^2$ が任意の $\varepsilon >0$ に対して成立します. あとは $V[s^2$ ] を求めていきましょう. 定義から直ちに,

$\begin{align} V[s^2] &= E[(s^2)^2]- E[s^2]^2\\ &= \dfrac{1}{(n-1)^2} \int_{\mathbb{R}^2}\left( \sum_{i=1}^n (x_i -\bar{x})^2\right)^2 F(x)\,dx -\sigma^4 \end{align}$

が従います. ただし $\bar{x} = \frac{x_1 + \cdots +x_n}{n}$ , $F(x) = f(x_1)f(x_2)\cdots f(x_n)$ です（前回参照）. また, $\sigma^4$ は正確には $(\sigma^2)^2$ と書くべきところですがこのように表記しておきます. それではまずは括弧内の二乗を展開していきましょう.
\begin{align}
\sum_{i=1}^n (x_i -\bar{x})^2 &= \sum_{i=1}^n (x_i^2 -x_i \bar{x}+ \bar{x}^2)\\
&= \sum_{i=1}^n x_i^2 -n \bar{x}^2
\end{align}
ここで, $i$ が固定されているとき,
\begin{align}
\sum_{j=1}^n x_j = \left(x_i+\sum_{j\neq i}x_j\right)
\end{align}
であることに注意すれば, 右辺第２項は
\begin{align}
n \bar{x}^2&= \frac{1}{n} \sum_{i=1}^n x_i\sum_{j=1}^nx_j\\
&=\frac{1}{n} \sum_{i=1}^n x_i\left(x_i+\sum_{j\neq i}x_j \right)\\
&=\frac{1}{n} \sum_{i=1}^n x_i^2+\frac{1}{n} \sum_{\substack{1 \le i,j \le n \\ \#\{i,j\}=2}} x_ix_j
\end{align}
となります. ただしここで新しく表れた記法
\begin{equation}
\sum_{\substack{1 \le i,j \le n \\ \#\{i,j\}=2}}
\end{equation}
により $n(n-1)$ 通りの相異なる $i, j$ の選び方についての総和をあらわします. これにより
\begin{align}
\sum_{i=1}^n (x_i -\bar{x})^2
&= \sum_{i=1}^n x_i^2 -n \bar{x}^2\\
&= \frac{n-1}{n} \sum_{i=1}^n x_i^2 - \frac{1}{n} \sum_{\substack{1 \le i,j \le n \\ \#\{i,j\}=2}} x_ix_j
\end{align}
であり, 両辺2乗すると,
\begin{align}
\left(\sum_{i=1}^n (x_i -\bar{x})^2 \right)^2
&=\left( \frac{n-1}{n} \sum_{i=1}^n x_i^2 - \frac{1}{n} \sum_{\substack{1 \le i,j \le n \\ \#\{i,j\}=2}} x_ix_j \right)^2\\
&=\frac{1}{n^2} \Bigg( (n-1)^2\sum_{i=1}^n x_i^2 \sum_{j=1}^n x_j^2 \\
&\qquad -2(n-1) \sum_{i=1}^n x_i^2 \sum_{\substack{1 \le j,k \le n \\ \#\{j,k\}=2}} x_jx_k \\
&\qquad- \sum_{\substack{1 \le i,j \le n \\ \#\{i,j\}=2}} x_ix_j \sum_{\substack{1 \le k,\ell \le n \\ \#\{k,\ell\}=2}} x_kx_\ell\Bigg)
\end{align}
となります. 自乗と相異なるものの掛け算を区別したいので, それぞれの項をさらに変形し,
\begin{align}
\sum_{i=1}^n x_i^2 \sum_{j=1}^n x_j^2
&= \sum_{i=1}^n x_i^2\left(x_i^2+\sum_{j\neq i}x_j^2 \right)\\
&=\sum_{i=1}^n x_i^4 + \sum_{\substack{1 \le i,j \le n \\ \#\{i,j\}=2}} x_i^2x_j^2 ,
\end{align}
\begin{align}
\sum_{i=1}^n x_i^2\sum_{\substack{1 \le j,k \le n \\ \#\{j,k\}=2}} x_jx_k
&=\sum_{\substack{1 \le j,k \le n \\ \#\{j,k\}=2}} x_jx_k \left(x_j^2 +x_k^2+\sum_{i\neq j,k}x_i^2 \right)\\
&=\sum_{\substack{1 \le i,j,k \le n \\ \#\{i, j,k\}=3}} x_i^2 x_jx_k + \sum_{\substack{1 \le j,k \le n \\ \#\{j,k\}=2}} x_jx_k( x_j^2 + x_k^2)\\
&=\sum_{\substack{1 \le i,j,k \le n \\ \#\{i, j,k\}=3}} x_i^2 x_jx_k + 2\sum_{\substack{1 \le j,k \le n \\ \#\{j,k\}=2}} x_j^3x_k
\end{align}
という風に右辺第１項と第２項は変形されます. 最後の式変形では $( x_j^2 + x_k^2)$ は入れ替わりによって相異なる組み合わせが2回加算されることに注意しましょう. 第３項については, まず相異なる $i, j$ を任意に固定したとき,
\begin{align}
\sum_{\substack{1 \le k,\ell \le n \\ \#\{k,\ell\}=2}} x_kx_\ell
&= \left( x_i+x_j +\sum_{k\neq i,j} x_k \right) \left( x_i+x_j +\sum_{\ell \neq i,j} x_\ell \right) -\sum_{m=1}^n x_m^2\\
&= (x_i+x_j)^2 + 2(x_i +x_j) \sum_{k\neq i,j} x_k + \sum_{k\neq i,j} x_k\sum_{\ell \neq i,j} x_\ell \\
&\quad - \left(x_i^2 + x_j^2 +\sum_{m\neq i,j} x_m^2\right)\\
&= 2x_ix_j + 2(x_i +x_j) \sum_{k\neq i,j} x_k+ \left( \sum_{k\neq i,j} x_k\sum_{\ell \neq i,j} x_\ell -\sum_{m\neq i,j} x_m^2\right)
\end{align}
により,
\begin{align}
\sum_{\substack{1 \le i,j \le n \\ \#\{i,j\}=2}} x_ix_j \sum_{\substack{1 \le k,\ell \le n \\ \#\{k,\ell\}=2}} x_kx_\ell
&=2\sum_{\substack{1 \le i,j \le n \\ \#\{i,j\}=2}} x_i^2x_j^2 \\
&\quad +2 \sum_{\substack{1 \le i,j \le n \\ \#\{i,j\}=2}} x_ix_j(x_i +x_j) \sum_{k\neq i,j} x_k\\
&\quad +\sum_{\substack{1 \le i,j \le n \\ \#\{i,j\}=2}} x_ix_j \left( \sum_{k\neq i,j} x_k\sum_{\ell \neq i,j} x_\ell -\sum_{m\neq i,j} x_m^2\right)\\
&=2\sum_{\substack{1 \le i,j \le n \\ \#\{i,j\}=2}} x_i^2x_j^2 \\
&\quad +4 \sum_{\substack{1 \le i,j,k \le n \\ \#\{i,j,k\}=3}} x_i^2x_jx_k\\
&\quad +\sum_{\substack{1 \le i,j,k,\ell \le n \\ \#\{i,j,k,\ell\}=4}} x_ix_j x_kx_\ell
\end{align}
を得ます. $\displaystyle\sum_{\substack{1 \le i,j,k \le n \\ \#\{i,j,k\}=3}} = n(n-1)(n-2)$ , $\displaystyle\sum_{\substack{1 \le i,j,k,\ell \le n \\ \#\{i,j,k,\ell\}=4}} = n(n-1)(n-2)(n-3)$ なので, 以上をまとめれば,

$\begin{align} &\dfrac{1}{(n-1)^2} \int_{\mathbb{R}^2}\left( \sum_{i=1}^n (x_i -\bar{x})^2\right)^2 F(x)\,dx \\ &\quad= \frac{1}{n^2(n-1)^2}\int_{\mathbb{R}^n} dxF(x) \\ &\qquad\Bigg[ (n-1)^2\left(\sum_{i=1}^n x_i^4 + \sum_{\substack{1 \le i,j \le n \\ \#\{i,j\}=2}} x_i^2x_j^2\right)\\ &\qquad -2(n-1)\left(\sum_{\substack{1 \le i,j,k \le n \\ \#\{i, j,k\}=3}} x_i^2 x_jx_k + 2\sum_{\substack{1 \le j,k \le n \\ \#\{j,k\}=2}} x_j^3x_k\right)\\ &\qquad +\left( 2 \sum_{\substack{1 \le i,j \le n \\ \#\{i,j\}=2}} x_i^2x_j^2+4 \sum_{\substack{1 \le i,j,k \le n \\ \#\{i,j,k\}=3}} x_i^2x_jx_k+\sum_{\substack{1 \le i,j,k,\ell \le n \\ \#\{i,j,k,\ell\}=4}} x_ix_j x_kx_\ell\right) \Bigg]\\ &\quad=\dfrac{1}{n^2(n-1)^2} \Bigg( n(n-1)^2 \mu_4 -4n(n-1)^2 \mu_1 \mu_3 + n(n-1)(n^2-2n+3)\mu_2^2 \\ &\qquad \qquad -2n(n-1)(n-2)(n-3)\mu_1^2 \mu_2 + n(n-1)(n-2)(n-3)\mu_1^4\Bigg)\\ &\quad= \frac{1}{n}\left(\mu_4 -4\mu\mu_3 +3\mu^4+6\mu^2\sigma^2\right) +\frac{n^2-2n+3}{n(n-1)}\sigma^4 \end{align}$

以上により,

$\begin{align} V[s^2] &= \dfrac{1}{(n-1)^2} \int_{\mathbb{R}^2}\left( \sum_{i=1}^n (x_i -\bar{x})^2\right)^2 F(x)\,dx -\sigma^4\\ &=\frac{1}{n}\left(\mu_4 -4\mu\mu_3 +3\mu^4+6\mu^2\sigma^2\right) -\frac{n-3}{n(n-1)}\sigma^4\\ &\rightarrow 0 ,\quad \textrm{as } n\rightarrow \infty \end{align}$

これによりチェビシェフの不等式とあわせて

$\begin{equation} P(|s^2- \sigma^2| \ge \varepsilon) \rightarrow 0 ,\quad \textrm{as } n\rightarrow \infty \end{equation}$

が得られます. 以上により不偏標本分散 $s^2$ の一致性が証明されました.

添え字が異なるものを整理するのが結構面倒な証明でした. この記事と同様の解説は

標本分散、不偏分散が一致推定量であること

にもあります. また, $X$ が正規分布に従う場合は $s^2$ がカイ二乗分布に従うことを用いればかなり楽をすることができますし, さらにモーメント母関数の計算から3次, 4次モーメントはそれぞれ母平均と母分散で書けるのでもっと整理することが出来ます.

ついでにRにやらせてみよう

> ss = c()
> 
> M = 10000
> n = 5
> for (i in 1:M){
+ x = as.integer(runif(n,1,7))
+ m = mean(x)
+ y = (x - m)^2
+ S2 = sum(y)/4
+ ss <- append(ss, S2)
+ }
> 
> ss2 = cumsum(ss)/c(1:M)
> 
> plot(ss2, type = "l")
> abline(h=35/12)
>

f:id:wakabame:20180429072156p:plain
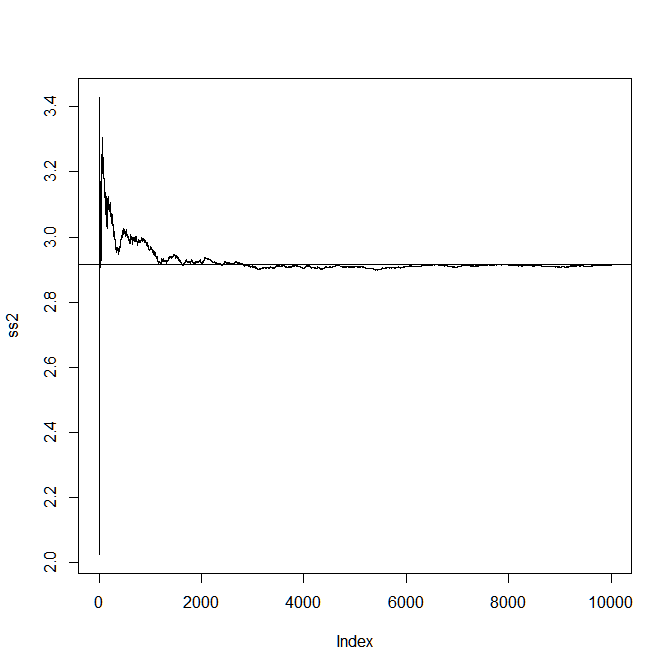
証明したとおり、不偏標本分散の平均は元の分散に漸近しているような感じがしますね！